A Picture Language in Elm

Background

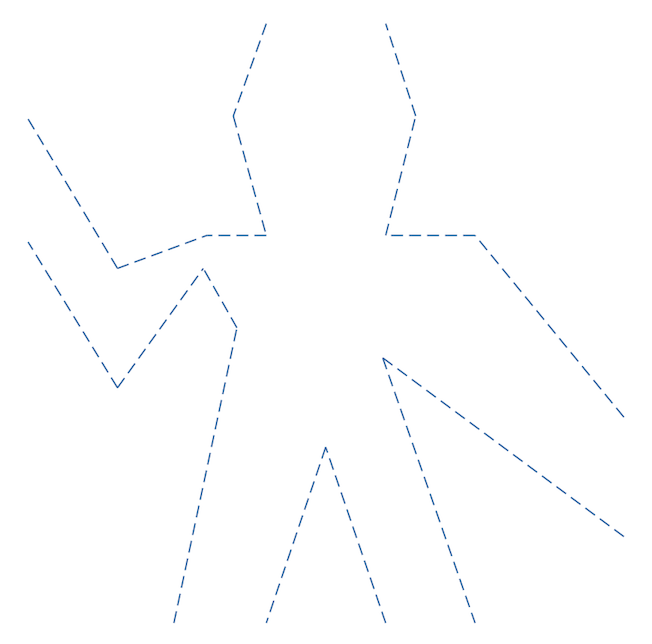
I remember I was fascinated by the example “A picture language”, while I was reading SICP. However, I was unable to try that example out on my own, due to my limited knowledge on Scheme or Lisp. Recently I am learning Elm, and while running some examples, I found it’s very easy to draw something on the browser. And the first thing I wanted to do is to simulate the picture language example using Elm. This example shows us how we can define some primitive operations, and build complex structure uniformly from those operations. We will start with a basic painter that looks like Figure-1.2.

Figure-1.1: Final result

After that we’ll define some procedures which transforms our basic painter to this beautiful, complex pattern shown in Figure-1.1. I recommend you to read the book example. Although reading that is not mandatory to follow the code examples here.

Figure-1.2: A primitive painter, wave

Vectors, Frames and drawLine

Let’s get started. First we define a type alias, Point, which is just a pair of Float.

Next we define three primitive vector operations for working with Points. Those are addVect for vector addition, subVect for subtraction, and scaleVect are for scaling vectors.

Elm is influenced by Haskell. We can give type annotation with each definition. Here addVect and subVect is taking two points as parameters and produces a new point. ScaleVect is taking a float and a point as parameter, and returns a point.

Next we define a record type called Frame. Frame has three properties, the origin, first edge and second edge.

Now we define the frameCoordMap function, as exactly defined in the book text. Here frameCoordMap takes two parameters, a frame and a Point. And it will map that point inside the frame, and return the coordinates of the mapped point. So that the point will be shifted and scaled to fit the frame.

Our primitive drawing operation is drawLine. We’ll use that operation to implement complex paint procedures. For implementing drawLine we are using Elm’s segment function from Graphics module. The segment function takes two coordinates and creates a path between them. And the traced function takes a LineStyle and a path and returns a Form. Combining these two we can write the following function.

We chose to return Form because it’s very flexible type in elm’s graphics module. We can combine a collection of Forms into a single Form which will come handy when we combine painters. Here |> is the forward function application, x |> f == f x. This function is useful for avoiding parenthesis, and writing code in a more natural way. We could write the drawLine function also like this.

But to me the former looks more readable. Now we are ready to define our painters.

Painters

We define the type Painter as a function. A function that takes a frame as parameter and returns a Form.

Notice the difference between Point/Frame and Painter. Where Point and Frame represents values, Painter represents a function. Invoking that function with a frame as parameter will produce our intended drawing. Representing Painter as function will turn out to be a powerful technique when we combine multiple painters.

The first painter we define is called segmentsPainter. It takes a list of line segments (start and end coordinate), and draws lines for each of the segments.

Notice the lambda notation represented by \frame ->. This means that segmentsPainter is returning a function. For each pair of coordinates we first map them inside the frame. And then call the drawLine function to draw a line between them. Finally we combine a list of Forms into a single form by using the group function.

Using the segmentsPainter we can define different kind of painters. For example the wave painter. The coordinate values for the wave painter is taken from Bill the Lizard’s page.

Let’s define a frame and call the main function to draw the wave painter like following. And we will get a image like Figure-1.2 as a result.

Transforming painters

Now we will write a function which will transform painters.

Explanation from the book.

Now we can use the transformPainter to define various transformations. For example the flipVert and flipHoriz like this.

Result of flipVert and flipHoriz on wave painter is shown in Figure-1.3.

Figure-1.3: flipVert and flipHoriz on wave painter

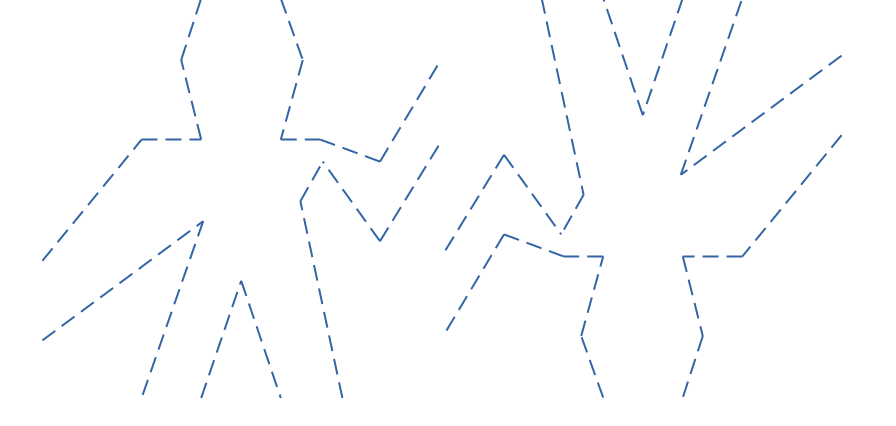
Next we define two more transformations, beside and below.

What below does is, it splits the frame into two half. And draws the two painters passed as parameters in one half each. Result of (beside wave (flipHoriz wave) is shown in Figure-1.4. The implementation of beside is very similar.

Figure-1.4: Result of (beside wave (flipHoriz wave))

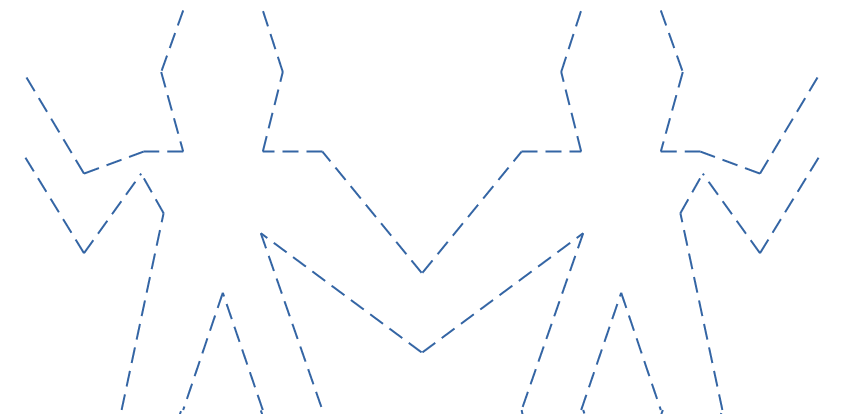
We can also define recursive functions as painters. For example we can define a painter which will split the initial painter in smaller part on each subsequent call.

The result of performing (rightSplit wave 6) is shown in Figure-1.5. Similarly we can also define another function upSplit, which will split the image recursively in upward location.

Figure-1.5: Result of (rightSplit wave 6)

We are pretty close to our final painter. We need to define one more transformer, cornerSplit.

CornerSplit is a simple recursive function. We are calculating the smaller pieces, and placing them appropriately. Result of performing (cornerSplit wave 6) is shown in Figure-1.6.

Figure-1.6: Result of (cornerSplit wave 6)

Finally we define the squareLimit function as below.

It is also a simple function where we are computing the smaller parts (quarter and half) of the frame. And then combining the smaller parts to form the final painter. Now we can apply the squareLimit function to our wave painter, and get the beautiful pattern shown in Figure-1.1.

Final thoughts

The important thing I learnt from this example is how various painter operations work in an uniform way. And we can build complex systems from very few basic operations.

You can view the full code here.